도도의 초록누리

[심심풀이(pastime)] 가정집 - 커튼 설치하기 with 치수측정

이번에 다뤄볼 내용은 실질적인 집에서 커튼을 어떻게 기장을 맞추고, 측정하고, 설치하는 지에 대해서 다뤄보고자 한다.

1. 목차

아래의 순서대로 다뤄보았다.

2. 환경 - 자연환경에 대한 사항

꼭 읽어보기 바란다.

3. 소개

작업 방법에 대해서 소개하였다.

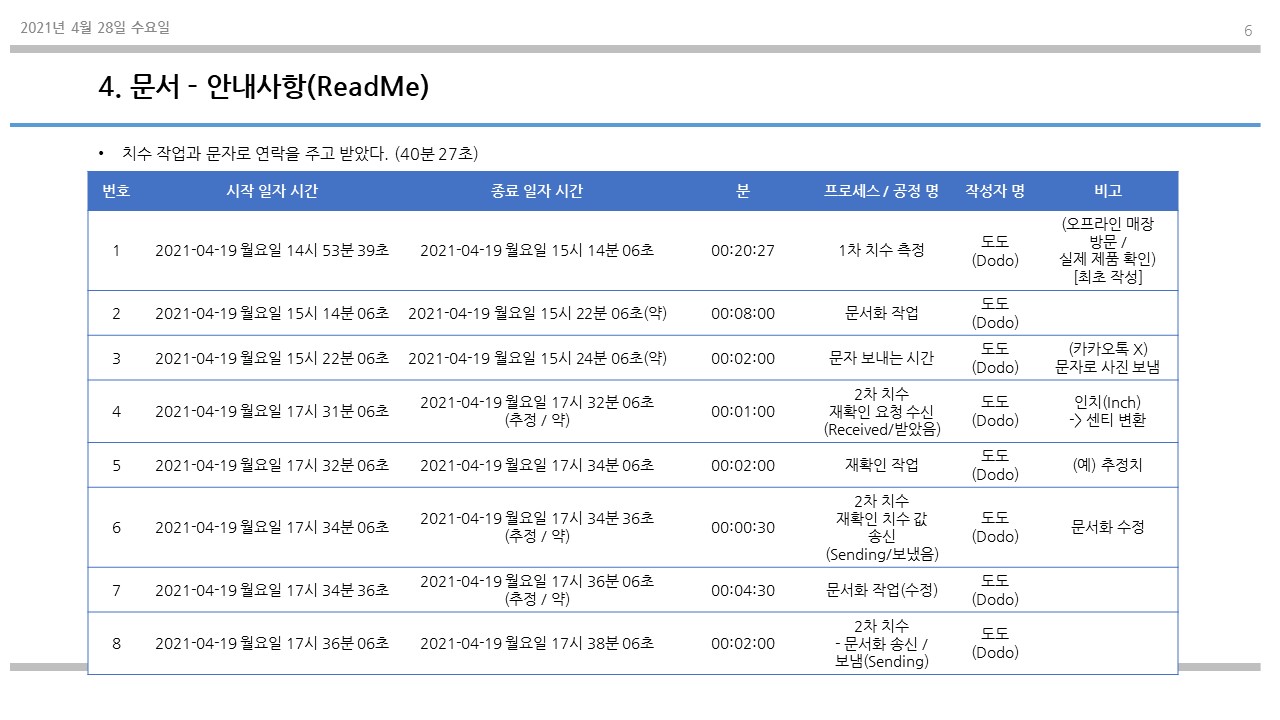
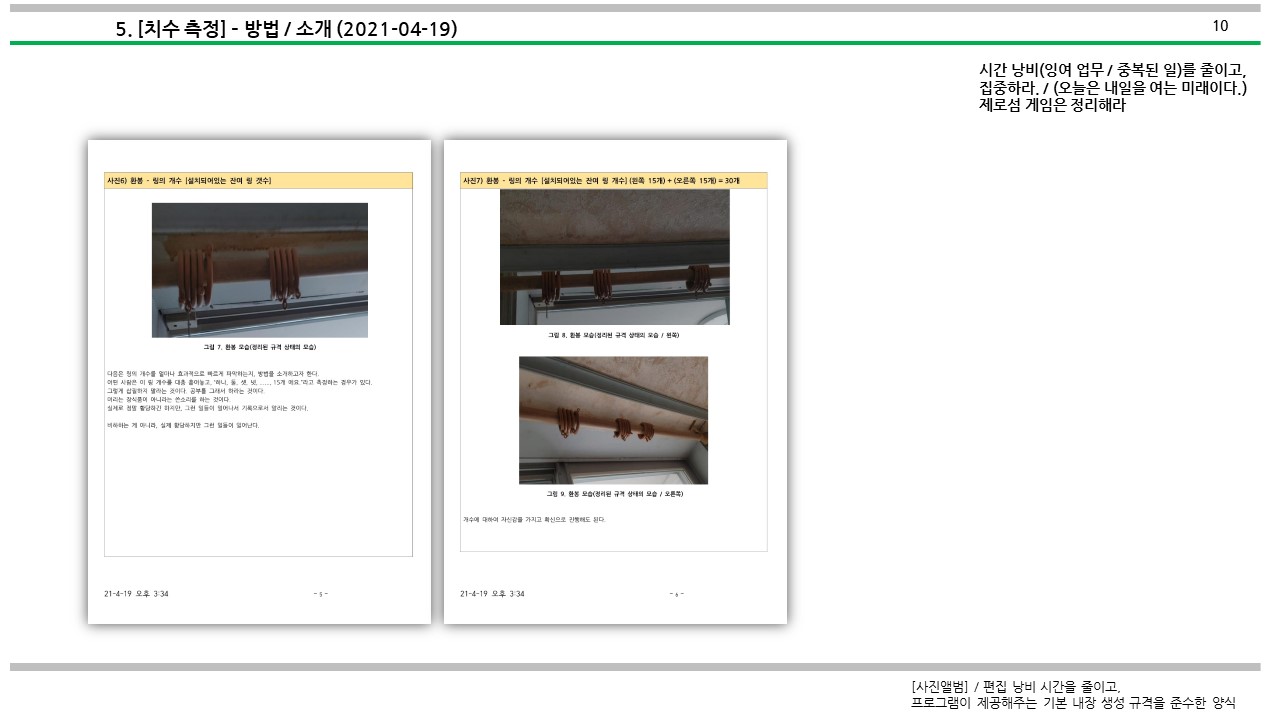
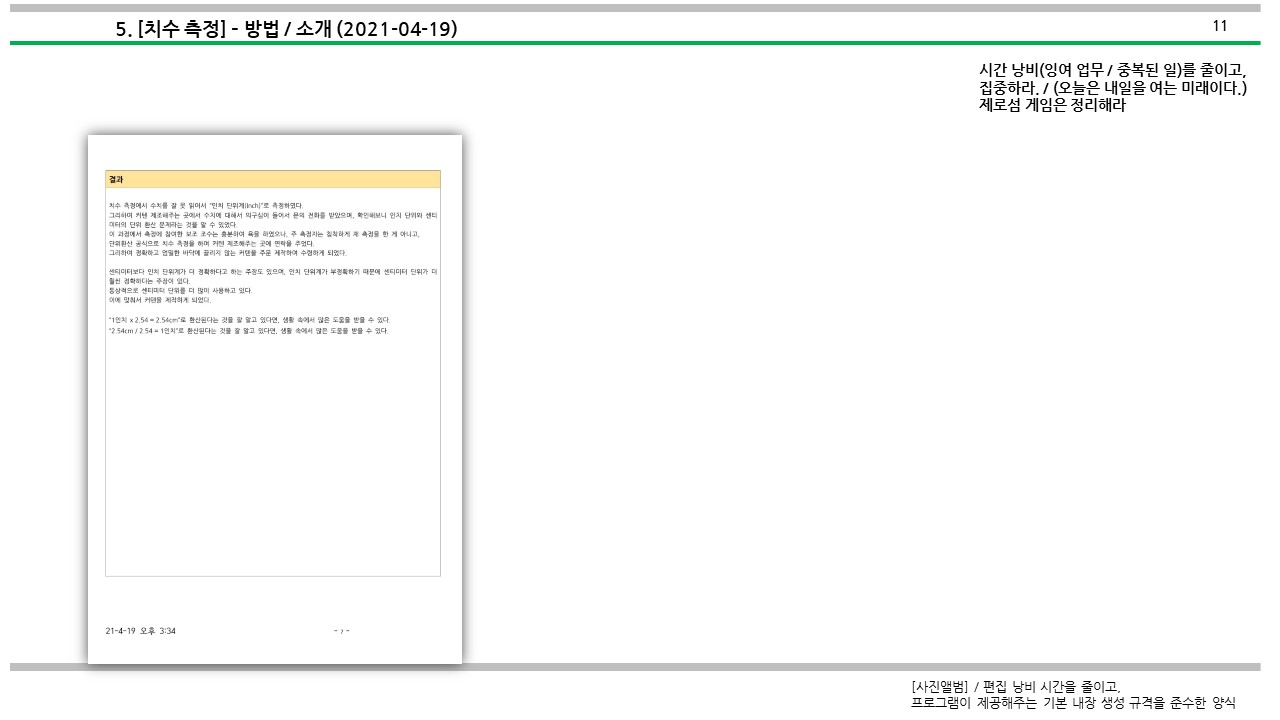
4. 첨부(Attachment) - 문서양식(Document Template)

(Mozilla Public License v2.0을 적용받는다.)

5. 첨부(Attachment) - 커튼 설치

(MPL(mozilla public License v2.0을 적용받는다.)

6. 맺음글(Conclusion)

치수 측정 및 커튼 설치에 대해서 자세히 살펴보았다.

* 참고자료(Reference)

1. 

[수학(Math)] 14. 역행렬(Inverse)

이 절에서는 정사각행렬 에 어떤 행렬을 곱하여 항등행렬이 되는 행렬에 대한 기본적인 성질에 대하여 살펴보기로 한다.

(예제) 행렬 에 대하여

이므로 이다.

정칙행렬의 역행렬은 유일하게 존재한다는 사실을 다음 정리에서 보일 수 있다.

정리:

= 유일하다.

의 역행렬이라 하자.

정사각행렬 가 정칙행렬이면 의 역행렬은 유일하게 존재한다.

(증명) 만일 가 의 역행렬이라고 가정하면

이다.

따라서 가 되어 의 역행렬은 유일하게 존재한다.

임의의 정사각행렬 에 대하여 역행렬이 반드시 존재하는 것은 아니다. 다음의 예제를 살펴보자.

(예제) 행렬 의 역행렬이 존재한다고 가정하고 그 역행렬을 라고 하면 다음이 성립한다.

따라서

이다. 그런데 이 식을 만족시키는 실수 는 존재하지 않는다. 따라서 행렬 가 행렬 의 역행렬이 된다는 사실에 모순이 된다.

즉, 행렬 는 정칙행렬이 아니다.

행렬 가 정칙행렬일 때 가 정칙행렬이라고 할 수 없다는 사실을 다음 예를 통하여 알 수 있다.

(예제) 두 행렬 와 는 정칙행렬이지만 이므로 는 정칙행렬이 아니다. 따라서 임의의 두 정칙행렬의 합은 정칙행렬이라고 할 수 없다.

(증명)

(1) 이므로 는 의 역행렬이다. 즉, 이다.

(2)

    이므로

   이다.

(3) 이므로 등식이 성립한다.

(예제) 두 행렬 와 는 정칙행렬이다. 또한

이므로

이다. 따라서 이고 이 성립한다.

(증명)

가 정칙행렬이므로 이다. 따라서,

이 되어 는 정칙행렬이고 이다.

(예제) 행렬 는 정칙행렬이고 역행렬은 이다. 또한

는 정칙행렬이고 역행렬은 이다. 따라서

(증명)

가 대칭행렬이므로 다음 관계가 성립한다.

따라서, 는 대칭행렬이 된다.

(예제)

행렬 에 대하여

이므로 는 대칭행렬이고 정칙행렬이다. 또한

이므로 의 역행렬 도 대칭행렬이다.

(증명) 가 교대행렬이므로 다음 관계가 성립한다.

따라서, 는 교대행렬이 된다.

(예제) 행렬 에 대하여

이므로 는 교대행렬이고 정칙행렬이다. 또한

이므로 의 역행렬 도 교대행렬이다.

[수학(Math)] 12. 행렬의 연산에 대한 성질

행렬들의 연산에 대한 기본적인 성질들에 대하여 살펴본다.

행렬들의 덧셈과 스칼라 곱셈, 그리고 상등관계의 정의에 의하여 집합 내에서 다음과 같은 성질이 성립함을 알 수 있다.

(정리1)
세 행렬  와 실수 에 대하여 다음이 성립한다.

 

 

[증명]

행렬의 곱이 정의된다고 가정했을 때 실수에서 결합법칙과 배분법칙이 성립하는 것과 마찬가지로 곱에 대한 결합법칙과 배분법칙이 성립한다는 것을 다음 정리에 의하여 알 수 있다.

(정리2)
행렬 와 에 대하여 다음이 성립한다.

[증명]

행렬의 성분을 각각 로 놓으면 의 -성분은 이므로

의 -성분은 이다.

또한, 행렬 의 -성분은 이고 의 -성분은 이므로 의 -성분은 이다. 따라서 행렬 와 의 -성분이 모두 같기 때문에 등식이 성립한다.

[증명]

행렬의 성분을 각각 로 놓으면 의 -성분은 이므로 의 -성분은 이다.

또한, 행렬 의 -성분은 이고 의 -성분은 이므로 의 -성분은

이다. 따라서 행렬 와 의 -성분이 모두 같기 때문에 등식이 성립한다.

[증명]

각 행렬의 성분을 , , 으로 놓으면 행렬 의 -성분은 이므로

의 -성분은 이다.

또한, 행렬 의 -성분은 이므로 의 -성분은

이다.

그런데

이므로 행렬 와 의 모든 -성분이 같다. 따라서 정리가 증명된다.

실수에서는 곱에 대하여 교환법칙이 성립하지만 행렬은 곱에 대하여 교환법칙이 성립하지 않는다는 사실을 다음 예제를 통하여 알 수 있다.

(예제)

다음 두 행렬의 곱 를 구하여라

[풀이]

행렬 을 각각 다음과 같이 놓자.

그러면

이다. 따라서 는 다음과 같다.

[수학(Math)] 10. 삼각함수표

수학에 관한 것이다.

삼각함수표에 대해서 가볍게 소개하려고 한다.

1. 삼각함수표의 구성

공학용 계산기에서의 sin(30)을 눌러보면 0.5의 값을 살펴볼 수 있다.

어떠한 체계로 구성이 되는지를 이해하려면, 호도법 또는 라디안(Radian)에 대해서 알 필요가 있다.

호도법과 삼각함수의 기초에 대해서 가벼운 수준에서 소개하였다고 본다.

스프레드시트를 열어서 sin(30)을 입력하면, -0.98xxxxxx의 수치를 확인할 수 있다.

그림 1-1. 삼각함수표의 예 - 도도(Dodo)

그림 1-1은 삼각함수표를 자연스럽게 표현한 것이다.

sin(Radian( ) )을 적용하게 된다면, 아래의 그림과 같이 삼각함수의 결과를 도출할 수 있다.

그림 1-2. 삼각함수 호도법 적용의 예 - 도도(Dodo)

그림 1-2는 삼각함수 호도법을 적용한 경우라고 보면 될 것 같다.

수학을 심도적으로 좋아하는 분이라면, 직접 만들어보는 것도 하나의 방법이 될 수 있다.

그림 1-3. 수동으로 식을 만들어서 해결한 경우 - 도도(Dodo)

Sin 함수를 만드는 건 조금 복잡할 것 같다.

radian 정도는 가볍게 만들 수 있을 것으로 보인다.

2. 삼각함수표 제작하기

삼각함수표를 제작하면 특이한 점을 관찰할 수 있다.

그림 2-1. 삼각함수표의 수치 비교 - 도도(Dodo)

radian()의 값이 달라질 수 있음을 알 수 있다.

그림 2-2. 삼각함수 시스템 (완성된 식과 수동으로 만든 식의 차이) - 도도(Dodo)

과학적 표기법에서는 유효숫자로 하여 수치를 처리하여 표현한다.

문제점은 정밀하고 엄밀한 수치를 추정할 수 있냐는 것이다.

[첨부(Attachment)]

TriangleTable.7z (ODS 파일)

3. 맺음글(Conclusion)

가볍게 삼각함수표가 왜 나오는지 이해하는 데 많은 도움이 되었으면 한다.

[수학(Math)] 9. 도함수와 적분(부정적분, 이중적분, 삼중적분)

Hi. My Name is Dodo.

안녕. 나의 이름은 도도야.

This article has written to begin for mathematics.

이 글은 수학을 입문을 위해 쓰여졌다.

1. 미분적분

미분적분은 Calculus(칼큘러스, 미분적분학으로 번역됨)에서 시작한다.

미분적분이 가지는 본연적 목적은 계산력 증진에 있다.

원리를 파악하려고 배우는 게 아니다. 미분적분을 응용하려고 해도 의미가 크게 없다.

수학에는 미분적분만 있는 게 아니다. 이산수학, 선형대수학, 대수학, 해석학, 기하학 등의 많은 공부 주제가 있다.

굉장히 많다는 이야기이다.

일반적으로 사용을 목적으로 하는 수학에서는 크게 고급적인 원리 증명을 요구하지 않은 것으로 알고 있다.

미분적분은 즉 계산력 증진을 위해서 사용한다.

라이프리츠와 뉴턴의 미분적분학이 고대에는 두 종류가 있었다. 발견을 비슷한 시기에 했었던 걸로 알고 있다.

결국은 라이프리츠의 방식을 채택하고 있지만, 일부 기호식에서는 뉴턴이 고안한 미분적분의 식이 현재에도 사용되고 있다.

예를 들면,

이러한 표기의 차이에서도 당시의 시대적인 상황을 느껴볼 수 있다.

2. 도함수

함수의 극한을 반드시 알아야 이해가 되는 것인가?

= ?

수열의 극한을 반드시 알아야 이해가 되는 것인가?

= ?

이 식으로 동작한다. 이 식을 정확히는 도함수라고 부른다.

흔히 이 식을 미분에 관한 식이라고도 부른다.

3. 부정적분

부정적분은 도함수를 역으로 하는 것이라고 표현한다.

다만, 학습을 하는데 있어서 편의상 그렇게도 부르는 경향이 있다.

크게 많은 식을 요구하지 않으며 이 식 하나면 정적분도 구할 수 있다.

4. 정적분

앞서 부정적분에 대해서 가벼운 식을 소개하였다. 정적분에 관한 식은 상한과 하한이 존재한다는 것이다.

아무래도 이런 점 때문에 함수의 극한 또는 수열의 극한을 권장하는 것으로 보인다.

그러나 계산에 의해서 해만 찾고 싶다면 이 식을 그냥 사용하는 것도 나쁘진 않다.

위에 있는 부정적분의 식을 그대로 사용한다.

간결하게 이런 느낌으로 사용하면 된다.

5. 이중, 삼중적분(Multi Integral)

이중적분, 삼중적분은 크게 어렵진 않다.

5-1) 이중적분

예1) 이중적분

이런 느낌으로 사용한다.

5-2) 삼중적분

말 그대로 적분을 3번 하는 것이다.

예1) 삼중적분

6. 맺음글

도도는 과연 이러한 식을 다 외우고 있는가?

= 자주 사용하지 않으면 모른다. 잊어버릴 때가 많다.

편안하게 접해보라고 작성한 것이다.

[수학(Math)] 5. 로그 (Log Arithmetric)

1. 생판 모른다고 전제하고 합니다. (I explained that if you beginner.)

이건.

읽기로는 "로그 2"라고 읽으면 됩니다. (Sound / Read : "Logarithm" "로그아팀")

앞서

라는 걸 배웠습니다.
 

이것도 0.30103 이 대략 나옵니다.

하나는 실제 로그표로 그래프 형태를 표현해보면.

예1) 실제 로그표를 그래프로 출력한 예

170116 - 예제2.ods  170116 - 예제2.xls  170116 - 예제2.xlsx

실제 로그 그래프를 출력함.

쉽게 이야기하면, 정밀한 데이타를 표현하기 위해서 (약~ "about~(읽기: 어바웃 / 대강 ~ 약)") 정도로

만들어 놓은 식 중 하나라고 보면 될 것입니다.

3. 로그에 대한 이야기?

앞서는

예를 들면,에 대해서 소개했습니다.

라고도 표현할 수가 있는데 과연 이런 형태만 있느냐. 그렇진 않습니다.

앞서 log X의 의미를 설명하면,

지금 두 데이타는 로 표현한 것과 표현한 것으로 볼 수 있습니다.